Project Pivot Point to Horizontal Line#

Suppose a hole is drilled underground into the back of a drift. The hole is drilled from a pivot point at a particular height from the floor. Typically this height is a characteristic of the drill. In itself, this is relatively moderate and quite standard in underground mining. Sometimes, the drill may break down, and they need to use a different drill. Suppose further that the alternate drill has a different pivot height from the floor. How can we determine where the new pivot point of each hole would be without re-designing the pattern? To narrow the scope a little, how can we determine the new horizontal distance of the pivot point from the reference line?

The idea is to show the horizontal distance from the reference line for a drill with pivots on a horizontal line at 2.15m from the floor. The mathematics will be developed for the general case solving for the horizontal distance of a new pivot point projected along the hole vector to a horizontal line.

The following diagram outlines the geometry that is used to derive the equation. It is based on similar triangles.

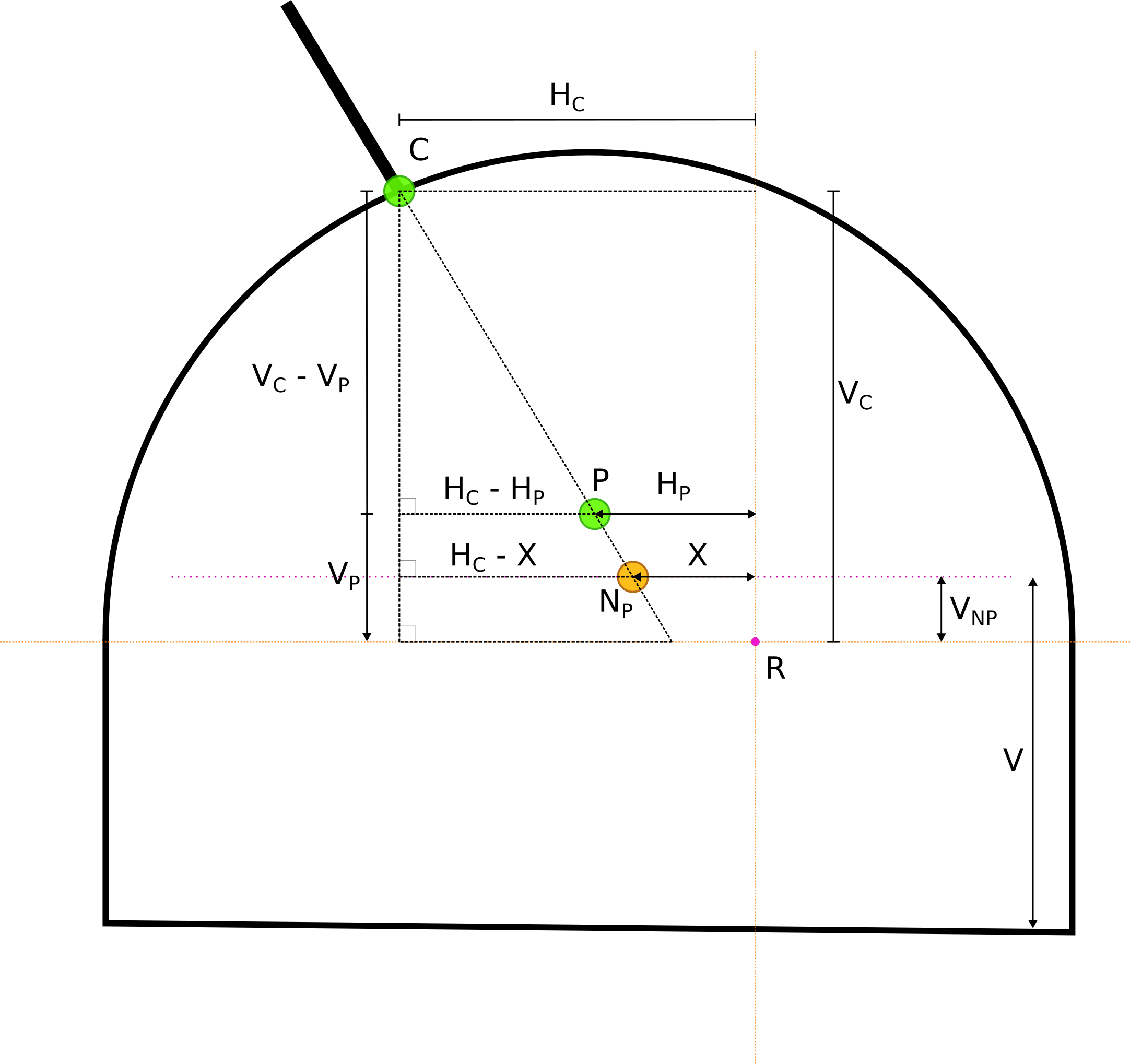
Definitions from the Image#

  • \(R\) - The point where the reference line intersects the ring plane. This is where the vertical and horizontal distances are measured for the collar and pivot points

  • \(C\) - The collar position of the hole

  • \(P\) - The hole pivot point (original)

  • \(N_P\) - The new pivot point based on the line defined by the height \(V\)

  • \(H_C\) - The horizontal distance of the collar from the reference line

  • \(V_C\) - The vertical distance of the collar from the reference line

  • \(V_P\) - The vertical distance of the pivot point from the reference line

  • \(H_P\) - The horizontal distance of the pivot point from the reference line

  • \(V\) - The distance from the floor to the horizontal line used by the alternate drill

  • \(X\) - The horiztonal distance of the new pivot, \(N_P\) from the reference line

  • \(V_{NP}\) - The vertical distance of the new pivot, \(N_P\) from the reference line

Solution#

This is a similar triangle problem, and we can equate the similar triangles and solve for \(X\).

(1)#\[\frac{H_C - H_P}{V_C - V_P} = \frac{H_C - X}{V_C - V_{NP}}\]

Solving for X:

(2)#\[X = H_C - \left(H_C - H_P \right) \left( \frac{V_C - V_{NP}}{V_C - V_P} \right)\]

Using Real Numbers from a Project (Hole is on the left-hand side of the reference line)#

  • \(H_C\) = -4.30

  • \(V_C\) = 2.88

  • \(V_P\) = 0.62

  • \(H_P\) = -3.45

We will use some Python to help with the math.

from pint import UnitRegistry
ureg = UnitRegistry()

Calculating \(V_{NP}\)#

Let us assume that the distance from the floor of the drift to the horizontal line is: \(V = 2.15 \text{m}\)

# HorizontalCollarOffset variable
HC = 4.30*ureg.meter

# VerticalCollarOffset variable
VC = 2.88*ureg.meter

# HorizontalPivotOffset variable
HP = 3.45*ureg.meter

# VerticalPivotOffset variable
VP = 0.62*ureg.meter


# User must supply this number
V  = 2.15*ureg.meter

# We need to know what the height of the reference line is from the floor of the drive. We can figure it out based on the pivot height and from the vertical pivot offset:

# `PivotHeight` custom formula variable
pivot_from_floor = 2.78*ureg.meter

# Height of reference line from floor
R = pivot_from_floor - VP

# We have enough information to calculate the vertical distance to the new pivot point on the horizontal line.

# Let us calculate V_np
v_np = V - R

# Display the results
print(f'R         = {R:.1f~P}')
print(f'v_np      = {v_np.to(ureg.mm):.1f~P}')

print(f'VP - v_np = {(VP - v_np):.3f~P}')

R         = 2.2 m
v_np      = -10.0 mm
VP - v_np = 0.630 m

Solving for X:

X = HC - (HC - HP)*((VC - v_np)/(VC - VP))
print(f'X = {X:.3f~P}')
# print(f'HP = {HP:.3f~P}')
# print(f'HP - X = {(HP - X).to(ureg.mm):.3f~P}')

X = 3.213 m

What Happens with a Vertical Hole?#

If we have a vertical hole \((H_C = 0)\), it is assumed that the pivot is vertical as well \((H_P = 0)\).

  • \(H_C\) = 0.0

  • \(V_C\) = 2.88

  • \(V_P\) = 0.62

  • \(H_P\) = 0.0

# HorizontalCollarOffset variable
HC = 0*ureg.meter

# VerticalCollarOffset variable
VC = 2.88*ureg.meter

# HorizontalPivotOffset variable
HP = 0*ureg.meter

  # VerticalPivotOffset variable
VP = 0.62*ureg.meter


# User must supply this number
V  = 2.15*ureg.meter

# `PivotHeight` custom formula variable
pivot_from_floor = 2.78*ureg.meter

# Height of reference line from floor
R = pivot_from_floor - VP

# Let's calculate V_np
v_np = V - R

X = HC - (HC - HP)*((VC - v_np)/(VC - VP))
print(f'X = {X:.3f~P}')

X = 0.000 m

This behaves as expected. The horizontal offset for the new pivot should be 0.

Can we use Negative Values to Give a Sense of Left and Right?#

Can we use the values from the custom formula variables directly and get a result that makes sense?

  • \(H_C\) = -4.30

  • \(V_C\) = 2.88

  • \(H_P\) = -3.45

  • \(V_P\) = 0.62

  # HorizontalCollarOffset variable
HC = -4.30*ureg.meter

# VerticalCollarOffset variable
VC = 2.88*ureg.meter


 # HorizontalPivotOffset variable
HP = -3.45*ureg.meter

# VerticalPivotOffset variable
VP = 0.62*ureg.meter

# User must supply this number
V  = 2.15*ureg.meter

# `PivotHeight` custom formula variable
pivot_from_floor = 2.78*ureg.meter

# Height of reference line from floor
R = pivot_from_floor - VP

# Let's calculate V_np
v_np = V - R

X = HC - (HC - HP)*((VC - v_np)/(VC - VP))
print(f'X = {X:.3f~P}')

X = -3.213 m

Negative values will work, and we can use the formula directly. That means using negative numbers to represent left-hand values will work.

Interest Rates - Interesting Properties