Average Cylinder Density#

Density is a straightforward concept, defined mathematically by the formula in equation (1). It represents the average mass per unit volume. When measuring density, it is typically assumed that the material is homogeneous and uniformly distributed within the volume. What if it wasn’t? I have some questions and math to examine the following questions:

  • What happens to the average density when two materials with different densities occupy the same volume?

    • That is, if I put one material on top of another material.

  • Can we calculate the proportions of each material needed to achieve a desired nominal density?

Density is defined as:

(1)#\[ \rho = \frac{m}{v} \]

Where:

  • \(\rho\) - Density in terms of mass per unit volume (g/cc, kg/m^3, lbs/ft^3)

  • \(m\) - Mass (g, kg, lbs)

  • \(v\) - Volume (cc, m^3, ft^3)

If we add two different materials to a cylinder, we have the scenario is illustrated in figure 1. In our case, let’s assume:

  • The volume of interest is a cylinder of length \(h\) and diameter \(d\).

  • We add two materials:

    • \(A\) with density \(\rho_a\) and height \(h_a\).

    • \(B\) with density \(\rho_b\) and height \(h_b\).

  • The materials do not mix.

Note

The math can easily be extended to multiple materials. This article does not explore that route.

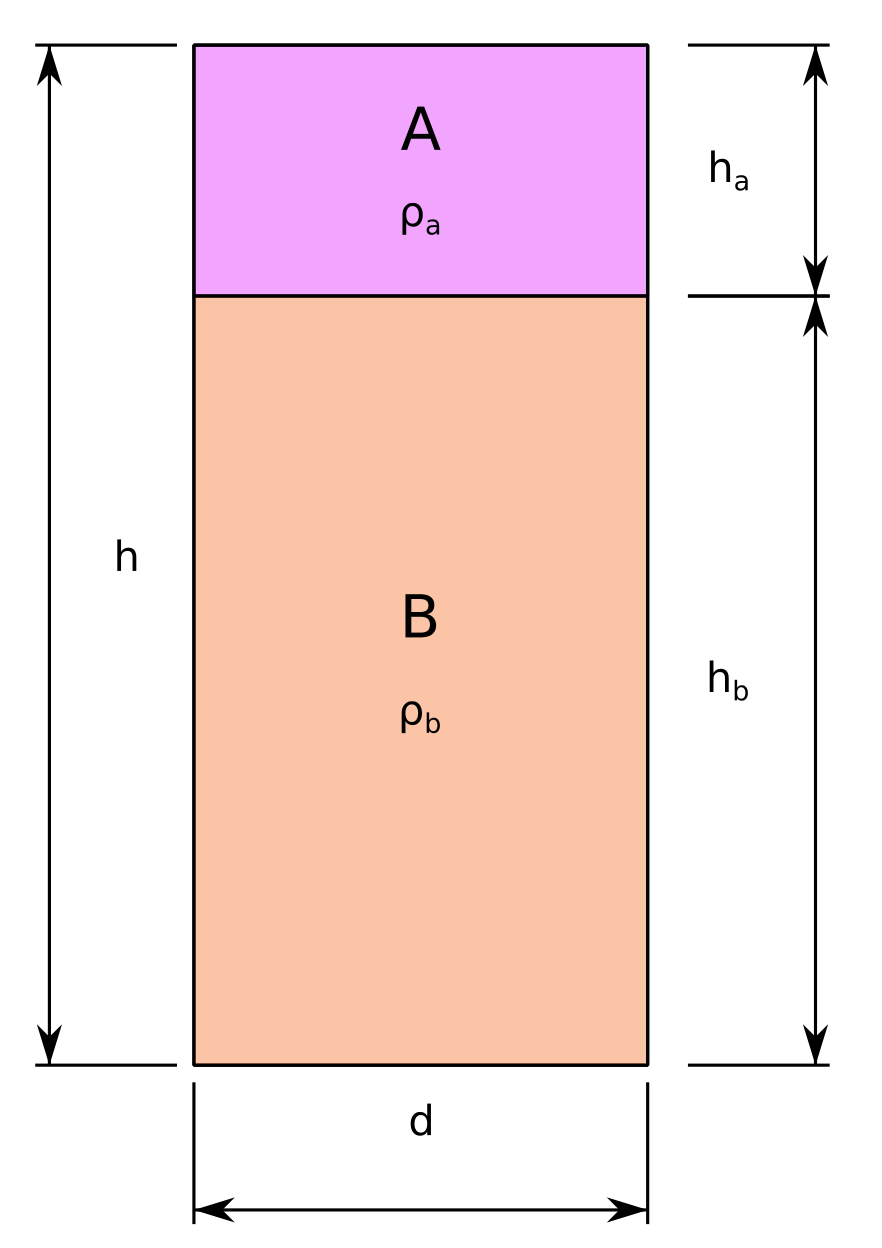
_images/cylinder_density.png

Schematic representing a possible configuration of two different products at different densities in a cylinder such that the average density is a certain value.#

The variables we’ll need to define are:

  • \(h\) - The cylinder height.

  • \(d\) - The diameter of the cylinder.

  • \(A\) - Material A.

  • \(B\) - Material B.

  • \(\rho_a\) - Density of material A.

  • \(\rho_b\) - Density of material B.

  • \(h_a\) - Height of cylindrical volume of material A.

  • \(h_b\) - Height of cylindrical volume of material B.

The volume of the cylinder is:

(2)#\[ V = \pi r^2 \cdot h \]

Where:

  • \(r\) - This is the radius of the cylinder and equal to: \(r = \frac{d}{2}\)

Average Density#

The average density is defined in equation (1). The average density of the two material system is defined in equation (6). We need to solve equation (6) and simplify the results.

(3)#\[ \rho_t = \frac{m_t}{V_t} \]
(4)#\[ m_t = m_a + m_b \]
(5)#\[ V_t = V_a + V_b \]

Using equations (4) and (5), we can expand (3) as follows:

(6)#\[ \rho_t = \frac{m_a + m_b}{V_a + V_b} \]

Where:

  • \(\rho_t\) - Average density of the cylinder.

  • \(m_t\) - Mass of the material in the cylinder.

  • \(V_t\) - Volume of the cylinder (total material volume).

  • \(m_a\) - Mass of material A.

  • \(m_b\) - Mass of material B.

  • \(V_a\) - Volume of material A.

  • \(V_b\) - Volume of material B.

(7)#\[ m_a = \rho_a \cdot V_a \]
(8)#\[ m_b = \rho_b \cdot V_b \]
(9)#\[ V_a = \pi r^2 \cdot h_a \]
(10)#\[ V_b = \pi r^2 \cdot h_b \]

Using (7), (8), (9), and (10):

\[\begin{split} \rho_t &= \frac{\rho_a \cdot V_a + \rho_b \cdot V_b}{\pi r^2 \cdot h_a + \pi r^2 \cdot h_b} \\ \rho_t &= \frac{\pi r^2 \cdot \left( \rho_a \cdot h_a + \rho_b \cdot h_b \right)}{\pi r^2 \cdot \left(h_a + h_b \right)} \end{split}\]
(11)#\[ \rho_t = \frac{\rho_a \cdot h_a + \rho_b \cdot h_b}{h_a + h_b} \]

The final average density can be calculated from (11) in terms of the height and density of each material.

Overall Target Density#

What if we had a target density for the whole cylinder, \(\rho_t\), and we knew the material densities, \(\rho_a\) and \(\rho_b\)? Can we determine \(h_a\) and \(h_b\)? Let’s rearrange (11) and see if we can figure it out.

\[\begin{split} \rho_t \cdot h_a + \rho_t \cdot h_b &= \rho_a \cdot h_a + \rho_b \cdot h_b \\ \rho_t \cdot h_a - \rho_a \cdot h_a &= \rho_b \cdot h_b - \rho_t \cdot h_b \\ h_a \cdot \left(\rho_t - \rho_a \right) &= h_b \cdot \left( \rho_b - \rho_t \right) \\ \end{split}\]
(12)#\[ \frac{h_a}{h_b} = \frac{\rho_b - \rho_t}{\rho_t - \rho_a} \]

Equation (12), shows the ratio of \(h_a\) and \(h_b\).

(13)#\[ h_a = \frac{\rho_b - \rho_t}{\rho_t - \rho_a} \cdot h_b \]

We know:

(14)#\[ h_t = h_a + h_b \]

Therefore, if we substitute (13) into (14) and simplify:

\[ h_t = \frac{\rho_b - \rho_t}{\rho_t - \rho_a} \cdot h_b + h_b \]
(15)#\[ h_t = h_b \cdot \left(1 + \frac{\rho_b - \rho_t}{\rho_t - \rho_a}\right) \]

Rearranging and solving for \(h_b\):

(16)#\[ h_b = \frac{h_t}{\left( 1 + \frac{\rho_b - \rho_t}{\rho_t - \rho_a} \right)} \]

If we know the shell dimensions, the densities of the materials and the average target density, we can solve for the height of the cylinder for material b, \(h_b\) (equation (16)). Once you know \(h_b\) you can solve for \(h_a\) using equation (14). If you are interested in the volume of either material cylinder use equation (9) and (10). If you want the mass of the material cylinders using equations (7) and (8).

To solidify the concept, let’s use a practical example:

  • \(\rho_t = 1.00 \, \frac{g}{\text{cc}}\)

  • \(\rho_a = 1.30 \, \frac{g}{\text{cc}}\)

  • \(\rho_b = 0.93 \, \frac{g}{\text{cc}}\)

  • \(h = 6.25 \, \text{inches}\)

  • \(d = 2.00 \, \text{inches}\)

Note

Normally, you would convert them so they are all using the same unit system. In this case, as long as the density units are the same and the length units are the same, there will not be a problem. The units cancel.

\[\begin{split} h_b &= \frac{6.25}{\left( 1 + \frac{0.93 - 1.00}{1.00 - 1.30} \right)} \\ h_b &= \frac{6.25}{\left(1 + 0.23 \right)} \\ h_b &= 5.08 \\ \end{split}\]

From equation (14), we have:

\[\begin{split} h_a &= h_t - h_b \\ h_a &= 6.25 - 5.07 \\ h_a &= 1.18 \\ \end{split}\]

Therefore, to achieve the target density of \(\rho_t = 1.00 \, \frac{g}{\text{cc}}\), \(h_b\) is 5.06 inches and \(h_a\) is 1.19 inches.

Further Thoughts#

It occurred to me, since I wrote the article yesterday, that equation (12) is not the most convenient form to work with. A ratio of both materials is not ideal. What would be convenient is a ratio of one of the material heights to the height of the cylinder. Something like this:

(17)#\[ \frac{h_b}{h_t} \]

From equation (17), we can see that:

(18)#\[ \frac{h_a}{h_t} + \frac{h_b}{h_t} = \frac{h_a + h_b}{h_t} = 1 \]

Why is the relationship in equation (18) valid? We have a cylinder of height, \(h_t\). We fill it with material a to a height of \(h_a\). We fill it with material b to a height of \(h_b\). From the diagram in figure 1, it follows that \(h_a + h_b = h = h_t\).

We can establish the material height ratios to the cylinder heights. We derive relationships from equation (18) in the following:

(19)#\[\begin{split} \frac{h_a}{h_t} &= 1 - \frac{h_b}{h_t} \\ \frac{h_b}{h_t} &= 1 - \frac{h_a}{h_t} \\ \end{split}\]

From equation (12), Let:

(20)#\[ \frac{h_a}{h_b} = \frac{\rho_b - \rho_t}{\rho_t - \rho_a} = r \]

This leads to:

(21)#\[ h_a = r \cdot h_b \]

Working from equation (19):

\[\begin{split} \frac{h_b}{h_t} &= 1 - \frac{r \cdot h_b}{h_t} \\ \frac{h_b}{h_t} + \frac{r \cdot h_b}{h_t} &= 1 \\ \frac{h_b \left(1 + r \right)}{h_t} &= 1 \end{split}\]
(22)#\[ \frac{h_b}{h_t} = \frac{1}{1 + r} \]

With equation (22) we have a solution in terms of the ratio of the material b height to the cylinder height. Let’s simplify and derive the final equation. Let:

\[ \frac{h_b}{h_t} = \frac{1}{1 + r} = \frac{1}{m} \]

Let:

\[\begin{split} m &= 1 + r = 1 + \frac{x}{y} \\ x &= \rho_b - \rho_t \\ y &= \rho_t - \rho_a \\ \end{split}\]
\[ m = 1+ \frac{x}{y} = \frac{y}{y} + \frac{x}{y} = \frac{x + y}{y} \]
\[\begin{split} m &= \frac{(\rho_b - \rho_t) + (\rho_t - \rho_a)}{\rho_t - \rho_a} \\ m &= \frac{\rho_b - \rho_a}{\rho_t - \rho_a} \\ \end{split}\]
\[ \frac{h_b}{h_t} = \frac{1}{m} = \frac{1}{\frac{\rho_b - \rho_a}{\rho_t - \rho_a}} \]

All of this simplifies to the final form:

(23)#\[ \frac{h_b}{h_t} = \frac{\rho_t - \rho_a}{\rho_b - \rho_a} \]

Equation (23) is the final form. This form places material height of b in a ratio with the height of the cylinder. It is more convenient to work with. We can use the equations listed in (19) to solve for the other material height ratio.

To confirm, let’s use the numbers from the previous section:

\[ \frac{h_b}{h_t} = \frac{1.00 - 1.30}{0.93 - 1.30} = 0.8108 \]
\[ h_b = 0.8108 \cdot 6.25 = 5.07 \]

The numbers match our previous calculations!

TDR and VOD Measurements