Circle/Ray Intersection#
The problem: We have a 2D circle and we have a ray or line. What are the intersections points between the two, if any?
There are many solutions, Google lists quite a few. The problem I found is that there were slight differences in the formulations and approaches and it took a great deal of effort to understand what exactly was happening. Most solutions did not include diagrams (which are extremely helpful) and not much background. I was looking for a vector based approach. There are a few, but they are not easy to read or understand. I used a number of different sources and approaches to construct this document. To me this makes sense, but it took quite a bit of work to get it to this point.
The solution I have used, and documented, to the problem is a vector based approach. We will determine the point on the ray that is closest to the center of the circle. This, by definition, will be perpendicular to the ray. If this distance is less than the radius of the circle, we will have two intersection points. From there it is a matter of solving the Pythagorean equation and constructing the intersection points.
There will be 3 cases for intersections:
No intersection between the ray and circle.
One intersection, that is the Ray will be tangent to the circle.
Two intersection points.
NOTE: This method will work for a general line as well as the directed Ray. It is a matter of determining the boundary conditions to apply and how to derive the solution for the intersection points.
Definitions#
We define the system as a circle with a center point, \(C = \left ( x,y \right )\) and radius \(r\). We define the Ray, \(R\) with a point, \(P\) on that ray and a direction vector, the unit vector, \(\vec{V}\). We want to solve for points \(P_1\) and \(P_2\) if they exist. The system is illustrated below in figure 1:
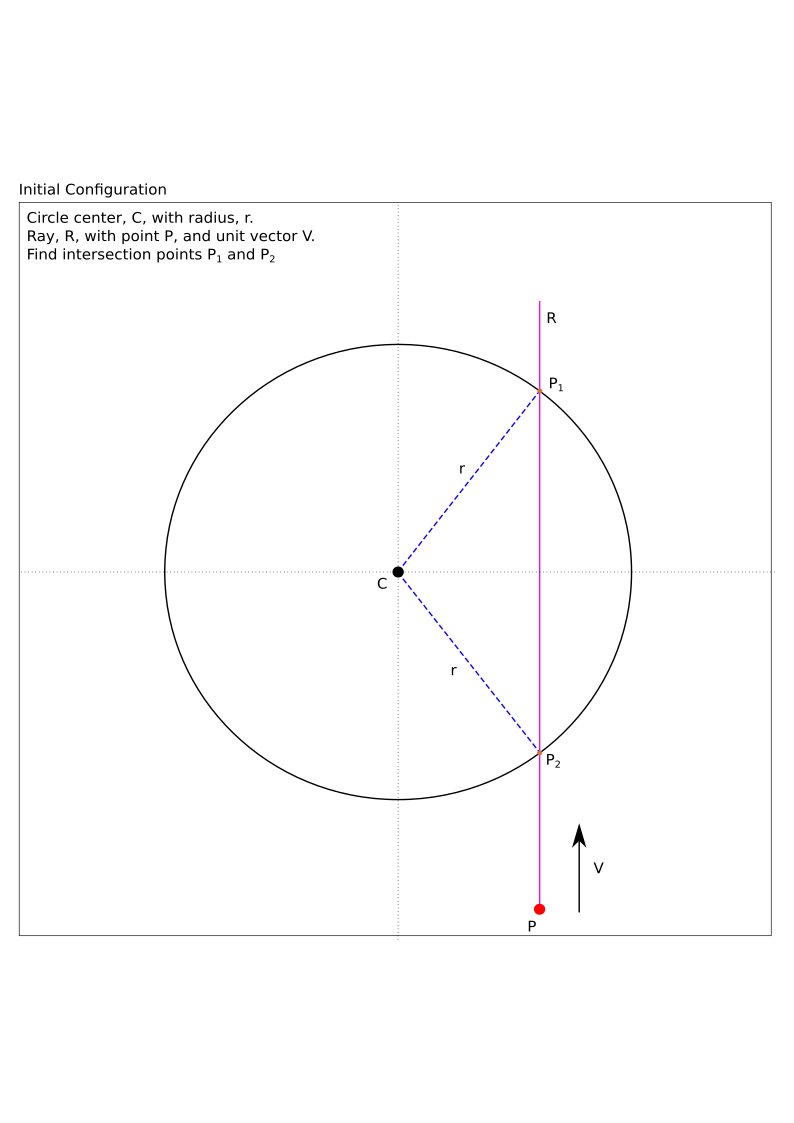
Figure 1 - System definition and configuration, circle center \(C\) and radius \(r\). The ray, \(R\) is defined by a point, \(P\) and a unit vector \(V\).#
Define \(\vec{U}\)#
We define a vector from the point \(P\) on the ray to the center of the circle, \(C\) (figure 2):
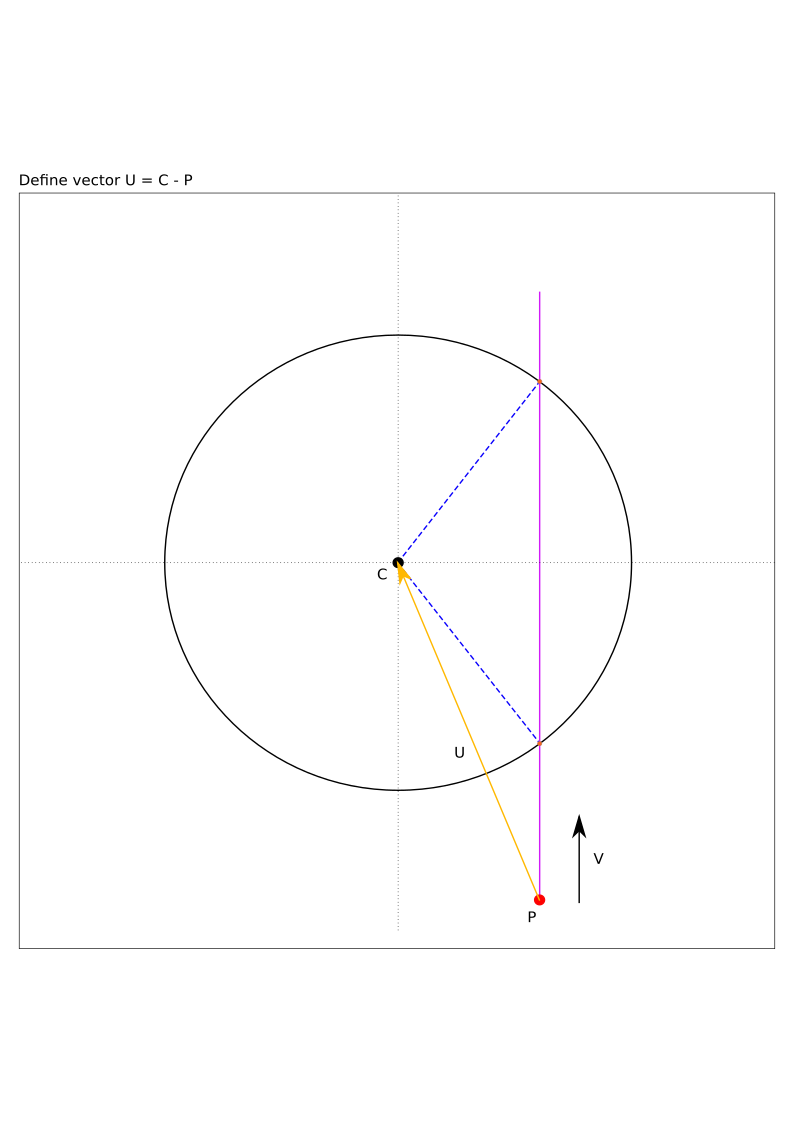
Figure 2 - Define \(\vec{U} = C - P\).#
Project \(\vec{U}\) onto \(\vec{V}\)#
We have \(\vec{U}\), how can this help us? If we project \(\vec{U}\) onto \(\vec{V}\) we will have a vector in the direction of \(\vec{V}\). The length of \(\vec{U}\) will end at a point that is the closest distance from the circle center!
Let’s project \(\vec{U}\) onto \(\vec{V}\) (figure 3):
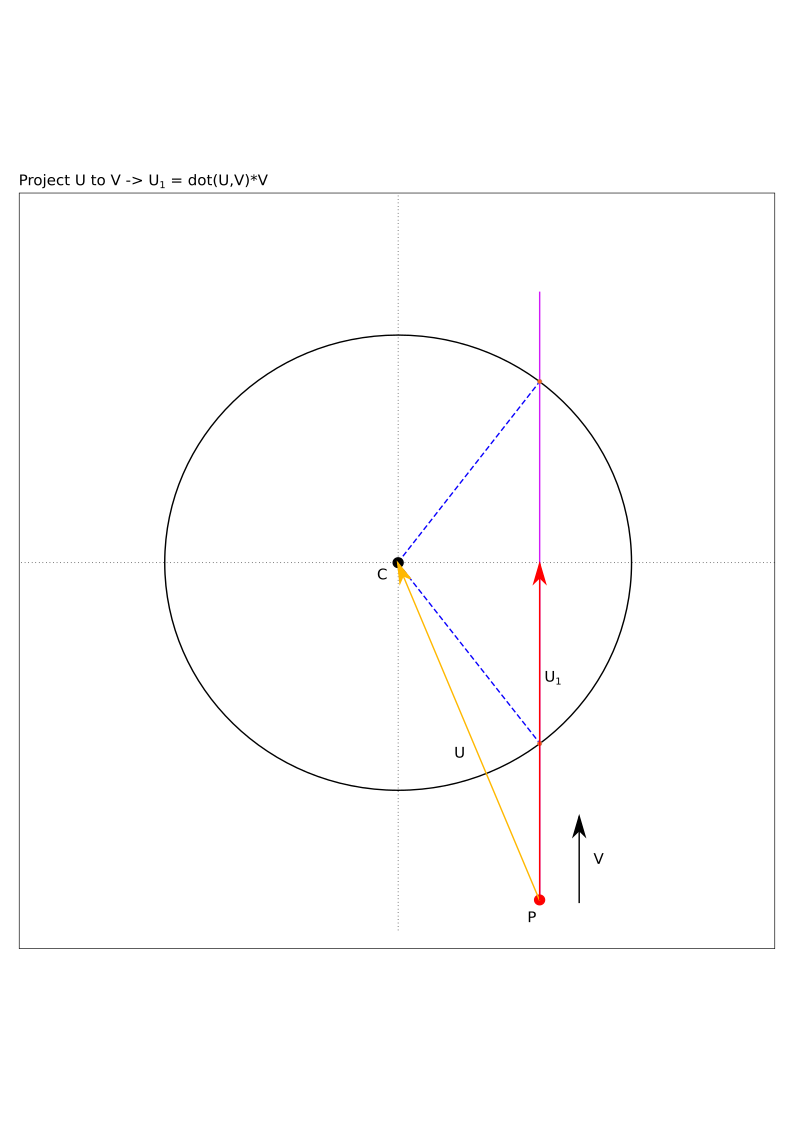
Figure 3 - Define \(\vec{U_1} = \left ( \vec{U} \cdot \vec{V} \right ) \vec{V}\)#
Note
We can also use this method to find the closest point on the Ray or Line to the circle. If we are interested in a line segment, we would use some logic to decide if the point is past one end or the other. Simply put it would be \(P_c = P + \vec{U_1}\). We could then perform a check or two see if that point falls on the line segment or the correct side of the Ray.
Distance to Circle Center#
Once we have \(\vec{U_1}\), we need to determine the vector to \(C\). We can do that by (figure 4):
Now that we have \(\vec{U_2}\), the norm of \(\vec{U_2}\) will be the closest distance from the Ray to the circle center. Calculate the distance, \(d\), by taking the norm of \(\vec{U_2}\) (figure 5):
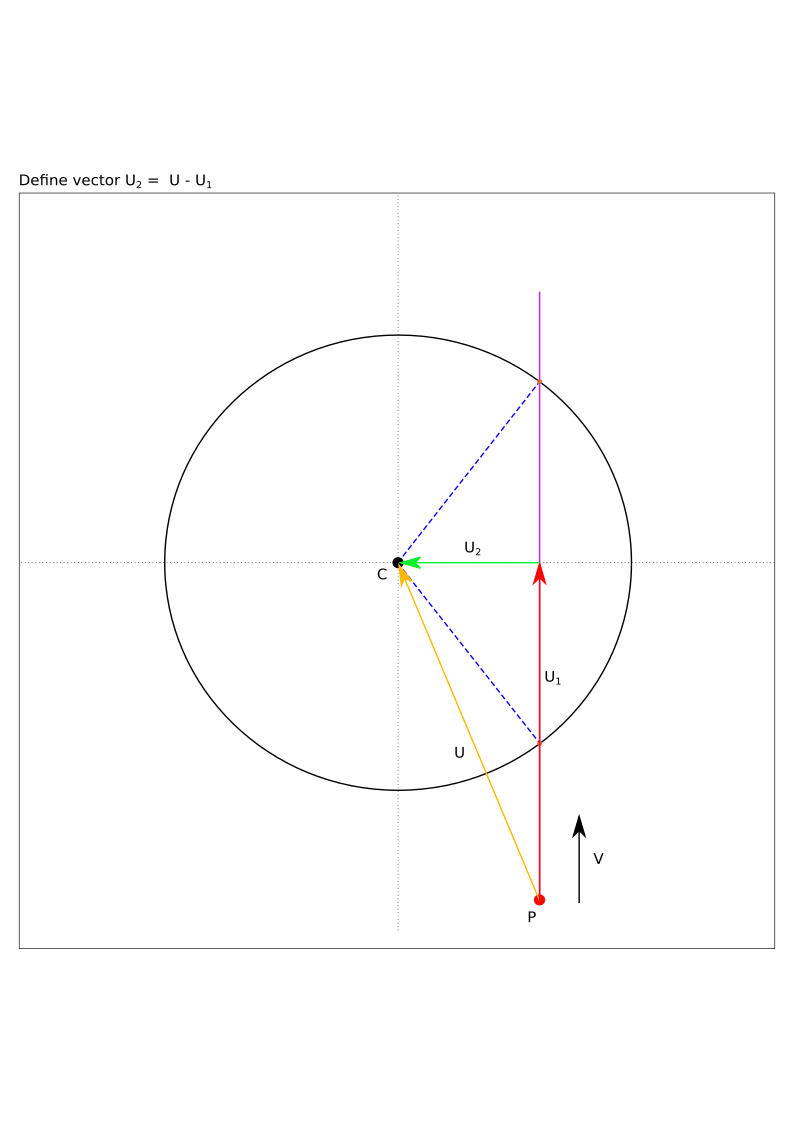
Figure 4 - \( \vec{U_2} = \vec{U} - \vec{U_1}\).#
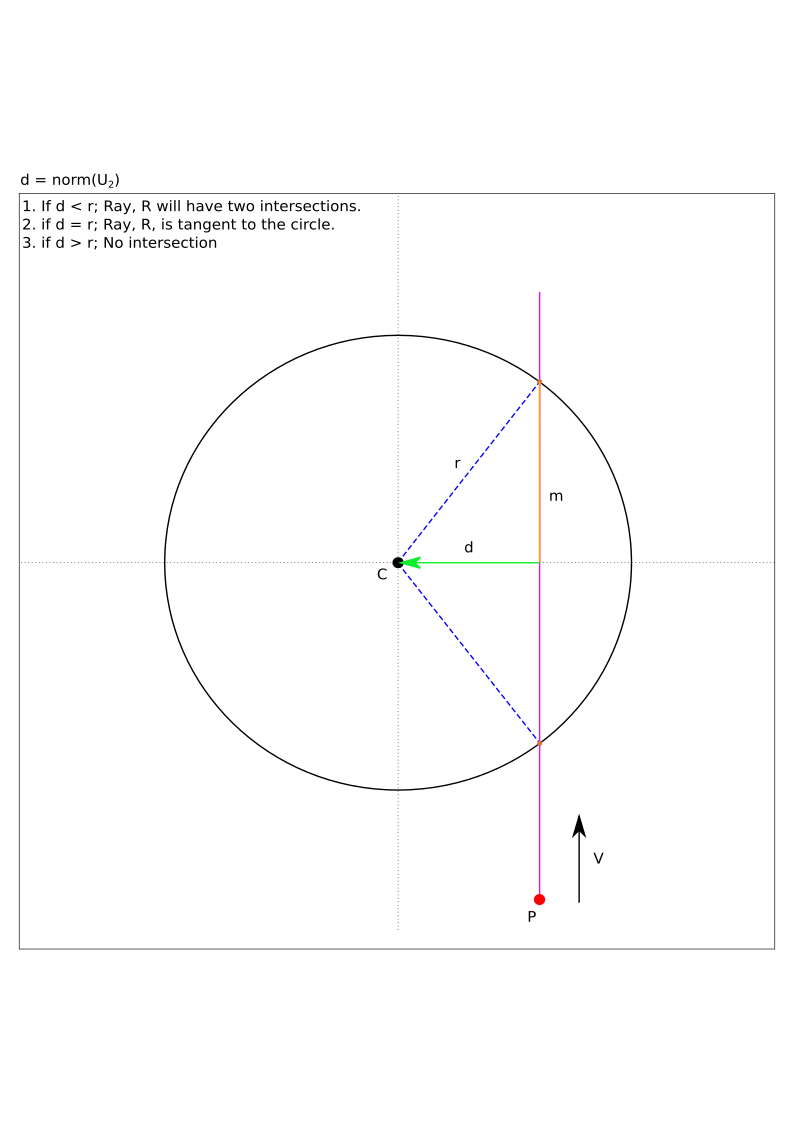
Figure 5 - \( d = \lVert \vec{U_2} \rVert \).#
At this point we have to decide what we are going to do:
if \(d \lt r\) we will have two intersection points.
if \(d = r\) we have the ray/line tangent to the circle.
if \(d \gt r\) we do not have an intersection.
Solve for Distance, \(m\)#
We can use the Pythagorean relationship to solve for the distance, \(m\) (figure 6). The distance, \(m\), will be used to derive the intersection points.
We calculate \(m\), by observing that it is part of the Pythagorean relationship:
Rearrange the equation to solve for \(m\) (figure 6):
Once we have \(m\), we can construct the intersection points (figure 7):
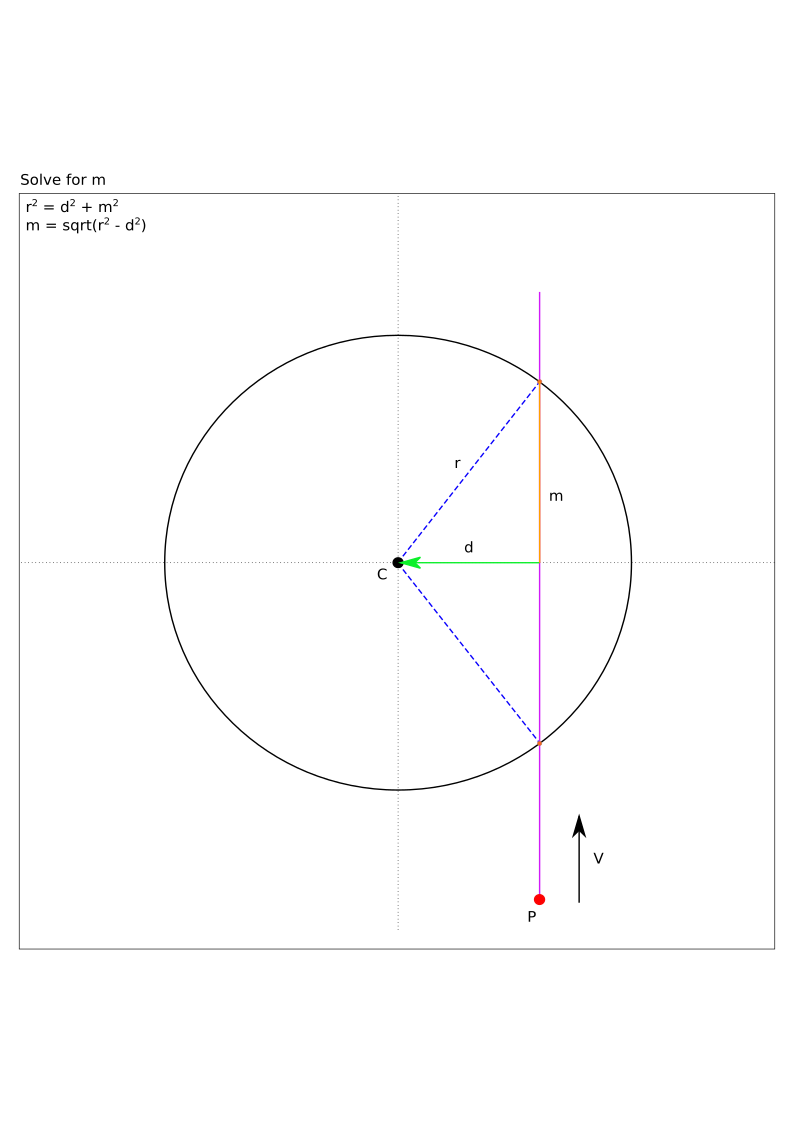
Figure 6 - Solve for \(m\).#
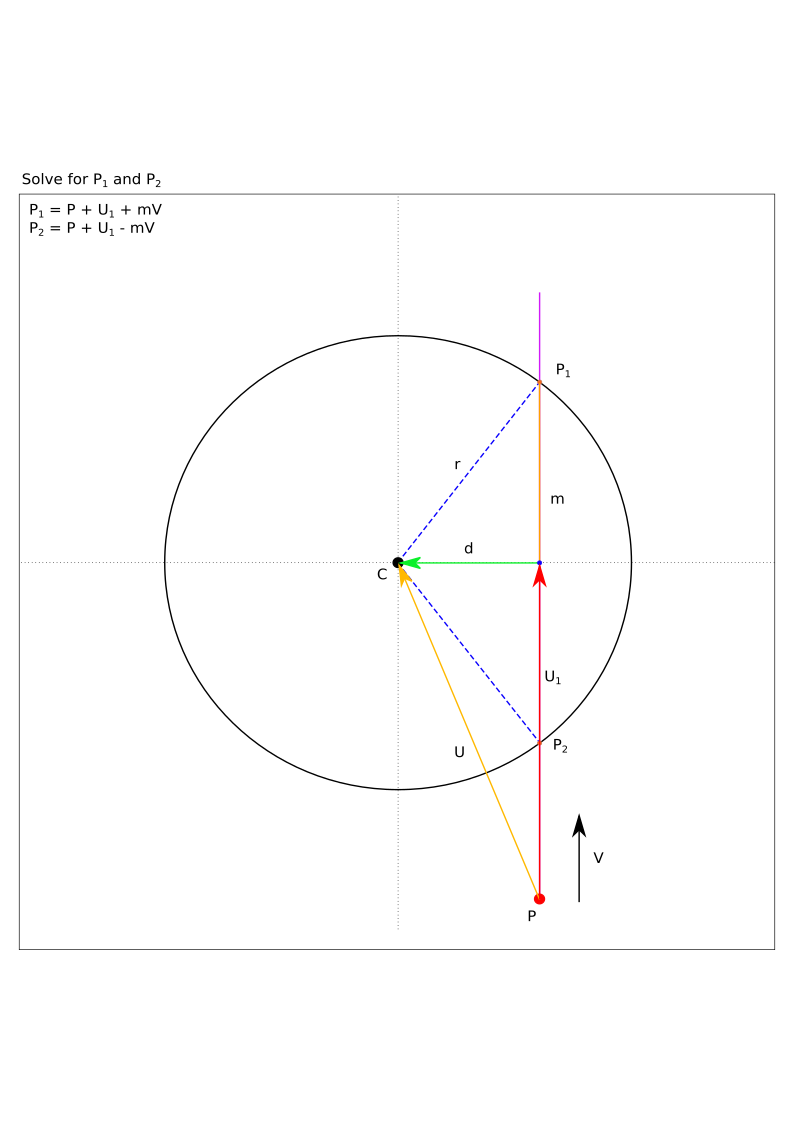
Figure 7 - Calculate \(P_1\) and \(P_2\).#
Example#
Here is a simple example using Python code:
C = Circle('C', Point2(0,0), 3.0)
R = Line(Point2(2.5, -4.0), Vector2(0,1))
U = C.center - R.point
# Project U onto V
U1 = U.dot(R.direction)*R.direction
# Vector to circle center
U2 = U - U1
d = U2.norm()
m = np.sqrt(C.radius**2 - d**2).item()
P1 = R.point + U1 + m*R.direction
P2 = R.point + U1 - m*R.direction
print(f'{U=}')
print(f'{U1=}')
print(f'{U2=}')
print(f'{d=}')
print(f'{m=}')
print(f'{P1=}')
print(f'{P2=}')
Output:
U=Vector2([-2.5, 4.0])
U1=Vector2([0.0, 4.0])
U2=Vector2([-2.5, 0.0])
d=2.5
m=1.6583123951777
P1=Point2([2.5, 1.6583123951777])
P2=Point2([2.5, -1.6583123951777])
Note
It is assumed that you have access to Vector2 and Point2 objects already defined.