

2024-08-18
In Canada, and many parts of the world, a car has high beam lights used for driving at night. They are much brighter than regular lights, and a driver should turn them off when a car is approaching. If it is not dictated by regulations, it is common courtesy to turn the high beams (or brights) off when on coming drivers are close enough.
I started to think, is it possible to tell how far a car (or object) is based on whether you can see two, distinct sources of light (left and right headlight) or one. What I was thinking, since a car has two headlights a fixed distance apart, can I estimate how far away it is?
Can we estimate how far away a car is based on whether we see one light or two?
The article will work through the mathematics and physics in an attempt to answer that question. The idea is to understand how far away the other driver is and how long to wait before turning the high beams off.
NOTE: The article was originally conceived and written on 2019-12-26.
To determine how far away the car is from the observer, we’ll make a few assumptions:
We will assume that the observer has normal visual acuity. Typically, on a Snellen chart, the width of the letters are about 5 arcseconds for 20/20 vision.
We will assume that the furthest distance we can see two lights separately is when the lights are 5 arcseconds apart or closer.
We assume perfect weather and atmospheric conditions. We ignore atmospheric conditions (heat distortions, thermoclines, bad weather, etc).
We assume a straight line distance with no elevation changes between the observer and vehicle (i.e. they are in the same lane heading towards each other). NOTE: In reality, they are in opposite lanes.
We will assume that the observer and car are travelling at a constant velocity, that is, no acceleration.
The observer will have normal 20/20 vision.
First, let’s define some relationships. One arcminute can be written as 1’. One arcsecond can be written as 1”. It is also worth noting that:
\[1 \, \text{arcminute} = \frac{1}{60}^\circ\]
\[1 \, \text{arcsecond} = \frac{1}{60}'\]
\[1 \, \text{arcminute} = \left ( \frac{1}{60} \right )^\circ \cdot \frac{\pi}{180^\circ} = \frac{\pi}{10800} \, \, \text{rad}\]
An arcsecond is a very small fraction of a degree. Land surveying regularly express angles in terms of degrees, minutes and seconds (DMS).
We are taking about how far a vehicle is away in terms of an angle.
What does that mean and why?
From fig. 1, we can see we are trying to determine the distance, \(D\), between the car and the observer. Unfortunately we cannot know what that is unless we can settle on an angle \(\theta\) that represent the distance between the headlights, \(d\). The angle between the headlights is a function of the distance between the headlights and the distance to the observer only.
NOTE: The further away the car is, the smaller the angle \(\theta\) will become.
However, people have a different levels of eyesight. For this particular article, we’ll assume that an average person can resolve two lights at an angle greater than 5 arcseconds. This means that if the angle between the headlights is 6 arcseconds, the person can see two distinct lights. If the angle is less than 5, the person will not be able to resolve two separate lights. It will look like one light or a blob or light connected.
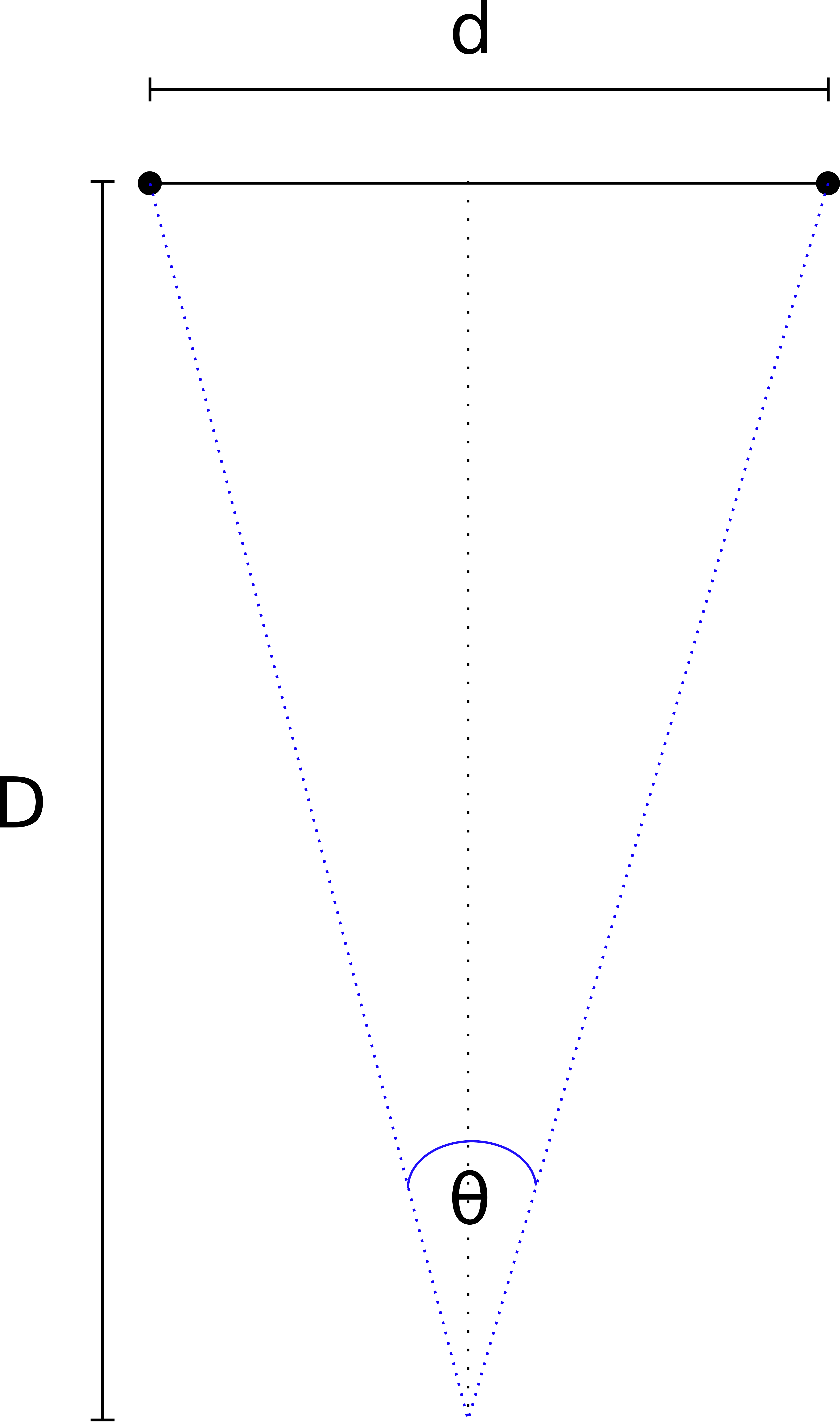
From fig. 1, we have:
\(D\) - The distance from the observer to the car.
\(d\) - The distance between the headlights of the car.
\(\theta\) - The angle as measured from each headlight to the observer. If it is less than 5 arcseconds, we consider the observer to only see one light source.
Let’s find a value for \(D\) such that \(\theta = 5 \, \text{arcseconds}\).
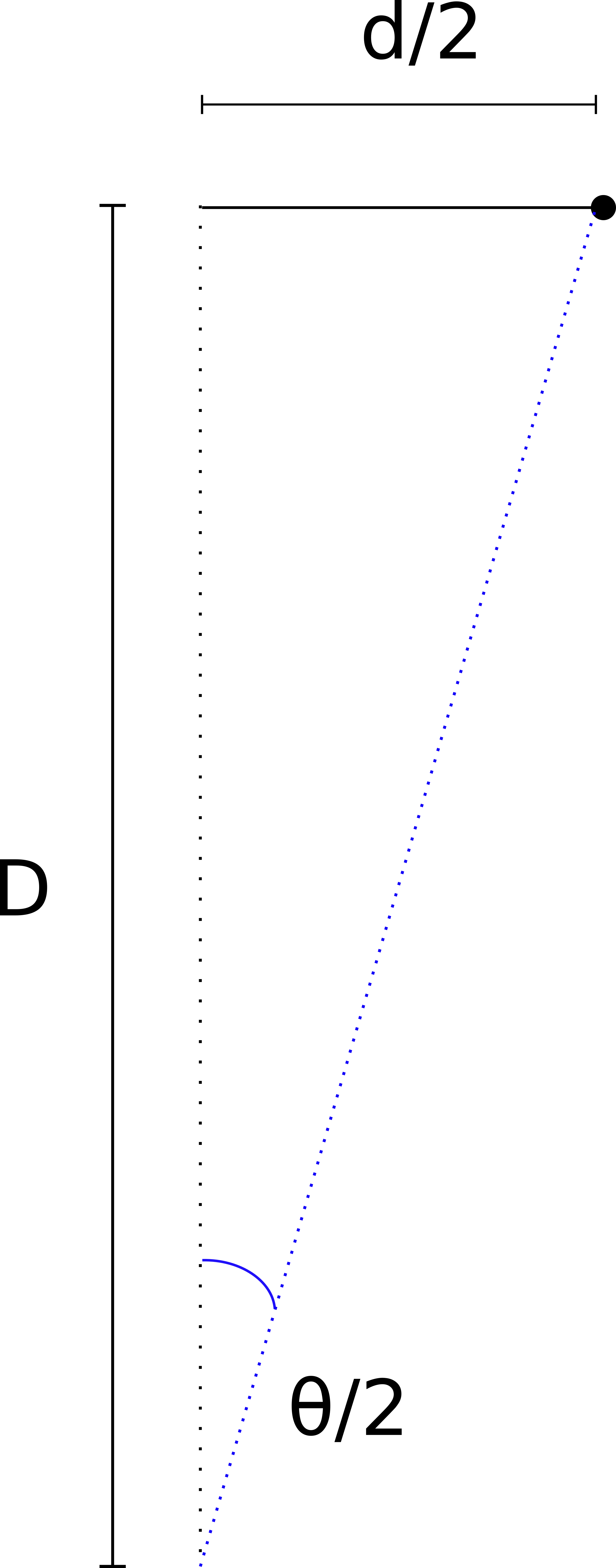
To find \(D\) for 5 arcseconds, we need to solve for the angle between the headlights. We can derive the angle as follows (fig. 2) :
\[\large \tan \frac{\theta}{2} = \frac{\frac{d}{2}}{D}\]
\[\large \tan \frac{\theta}{2} = \frac{d}{2 \cdot D}\]
\[\large \frac{\theta}{2} = \arctan \frac{d}{2 \cdot D}\]
\[\begin{equation} \large \theta = 2 \cdot \arctan \frac{d}{2 \cdot D} \end{equation}\]
Let’s solve for \(D\):
\[\large \tan \frac{\theta}{2} = \frac{d}{2 \cdot D}\]
\[\large 2 \cdot D = \frac{d}{\tan \frac{\theta}{2}}\]
\[\begin{equation} \large D = \frac{d}{2 \cdot \tan \frac{\theta}{2}} \end{equation}\]
Let:
import numpy as np
from pint import UnitRegistry
ureg = UnitRegistry()
d = 2*ureg['m']
theta = 5 * np.pi/10800
D = d/(2*np.tan(theta/2))
print(f'D = {D.to('m'):~.1f}')
print(f'D = {D.to("km"):~.1f}')D = 1375.1 m
D = 1.4 km
If two lights are placed at a distance of 2 meters apart, the average person would have to be further than 1.4 km before they would look like one light. In other words, a driver should be able to see one light source become two around 1.4 km away.
NOTE: That distance is highly dependent on the visual acuity of the observer and the atmospheric conditions (the astronomers would call it seeing) at the time.
d = 2*ureg['m']
theta = 5 * np.pi/10800
for angle in (10,5,1):
theta = angle * np.pi/10800
D = d/(2*np.tan(theta/2))
print(f'theta = {angle}')
print(f'D = {D.to('m'):~.1f}')
print(f'D = {D.to('km'):~.1f}')
print('--------')theta = 10
D = 687.5 m
D = 0.7 kmtheta = 5
D = 1375.1 m
D = 1.4 kmtheta = 1
D = 6875.5 m
D = 6.9 km
What we see is how close or far away people with worse or better eye sight would see one light resolve to two.
Now that we understand how far away the vehicle is, how long do we have before we should to turn off the high beams?

Assumptions:
Let’s assume that the observer is in a car, \(O\), and the other car, \(C\). Both cars are travelling at a constant velocity, \(V_1\) & \(V_2\), towards each other.
Each car is not accelerating. That is: \(\frac{dV_1}{dt} = \frac{dV_2}{dt} = 0\)
We will assume that we need to turn the high beams off when the distance between the two vehicles is \(m\)
The equation:
\[m = v \cdot t\]
Where:
We want to understand how long it will be before the other vehicle will be \(m\) from our vehicle. We can rearrange the equation:
\[t = \frac{m}{v}\]
Observe that both vehicles have 0 acceleration, and we can then treat one vehicle as stationary while the other approaches it at \(v = v_1 + v_2\).
\[\begin{equation} t = \frac{m}{v_1 + v_2} \end{equation}\]
Let:
\(v_1 = 90 \frac{km}{h}\)
\(v_2 = 90 \frac{km}{h}\)
\(m = 500 \, \text{m}\)
d = 2*ureg['m']
theta = 5 * np.pi/10800
D = d/(2*np.tan(theta/2))
print('Distance to see two headlights:')
print(f'D = {D.to('m'):~.1f}')
print(f'D = {D.to('km'):~.1f}')
print()
m = 500*ureg['m']
v1 = 90*ureg['km/h']
v2 = 90*ureg['km/h']
print('Distance to travel before turning off highbeams:')
print(f'{(D - m).to('m'):~.1f}')
print()
t = (D - m)/(v1 + v2)
print('Time to wait before turning off highbeams:')
print(f't = {t.to('s'):~.2f}')Distance to see two headlights:
D = 1375.1 m
D = 1.4 kmDistance to travel before turning off high beams:
875.1 mTime to wait before turning off high beams:
t = 17.50 s
Based on the assumptions, the observer should see the oncoming vehicle’s brights resolve to two headlights at about 1.4 km away. The observer should wait about 17 seconds or so before turning off the high beams to make sure that they are turned off at a reasonable distance, 500 m in this case.